
3 10 三角形面積公式的推導 Youtube
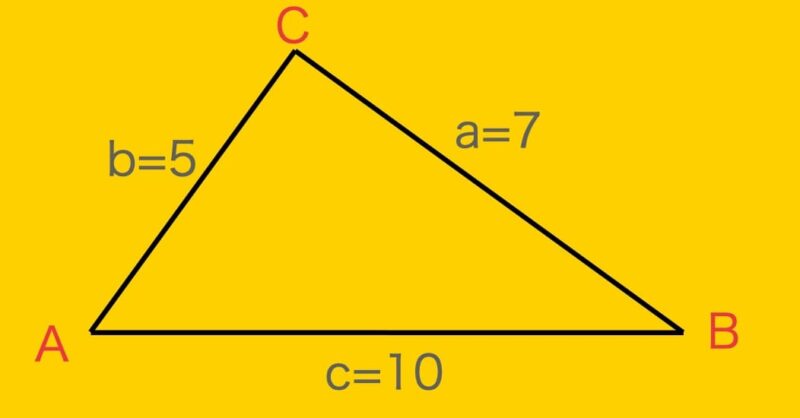
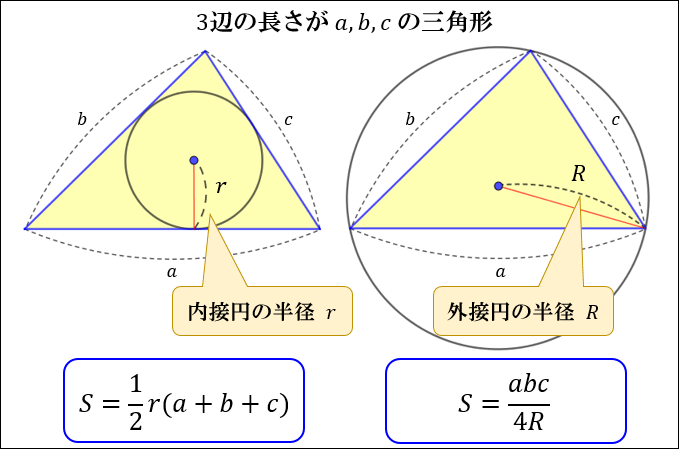
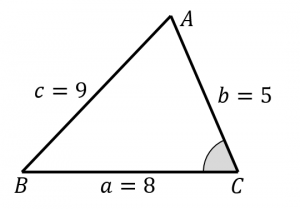
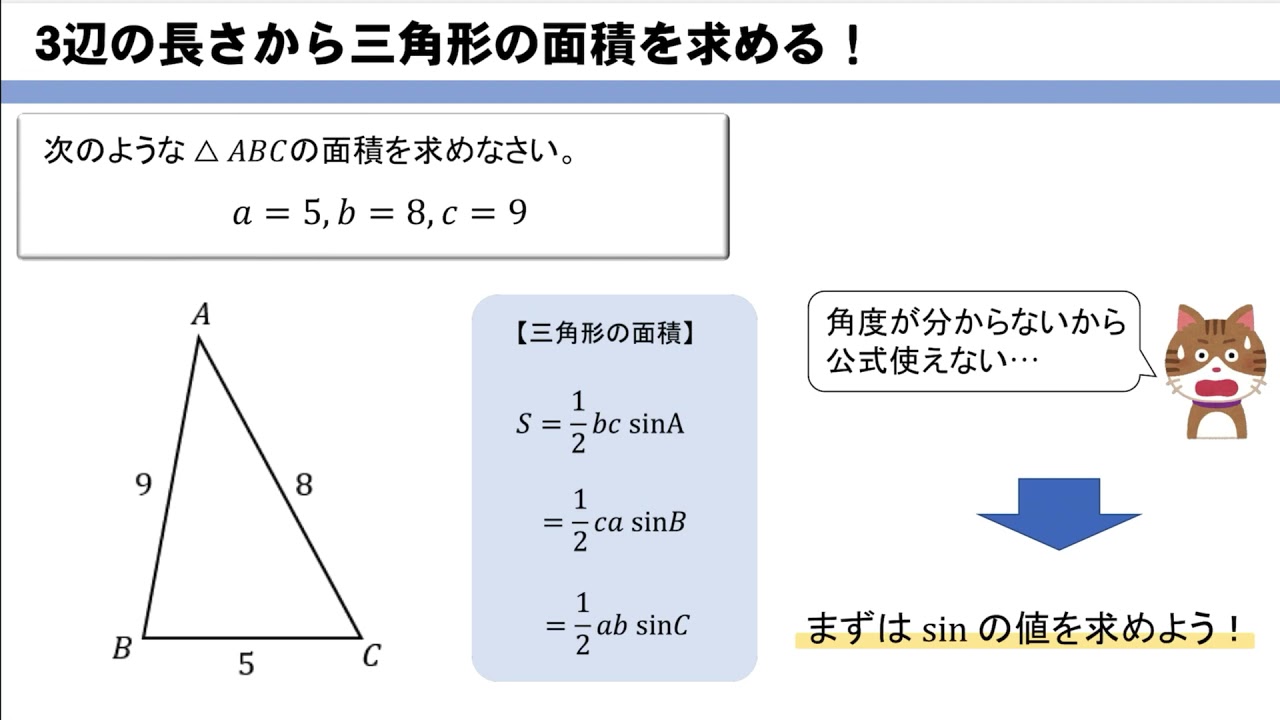
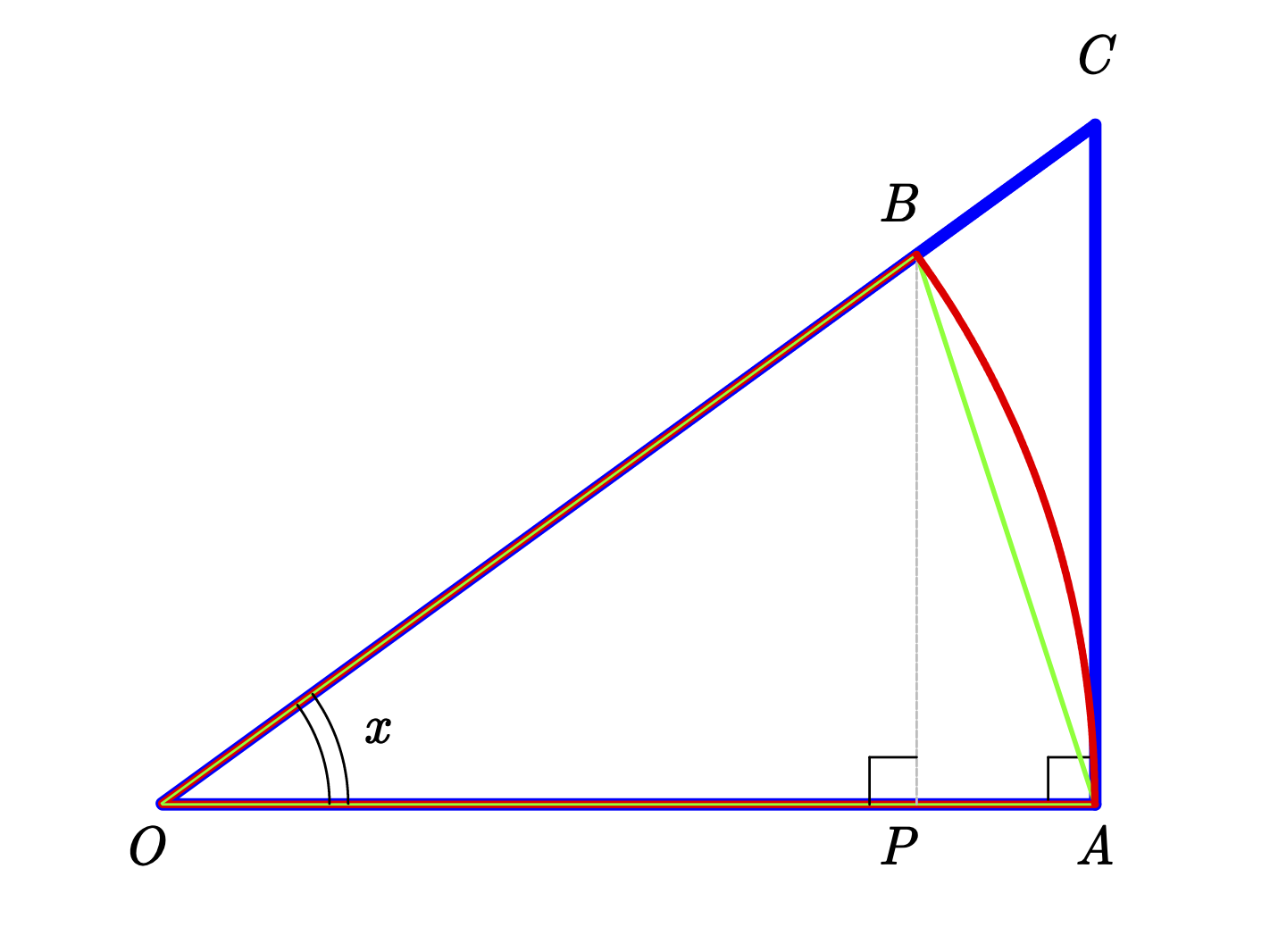
θ d θ の積分を図形を用いて直感的に理解する. 左側の図は 単位円 ,右側の図は y =sinθ y = sin θ のグラフである. 図において赤色の面積と青色の面積は等しい. ∫ π 2 0 sinθdθ ∫ 0 π 2 sin θ ヘロンの公式 3辺の長さが である三角形ABCの面積を は ただし である ヘロンの公式は「三角形の3辺が分かると、そこから面積が求まる」というすごい公式なのです! 三角形の
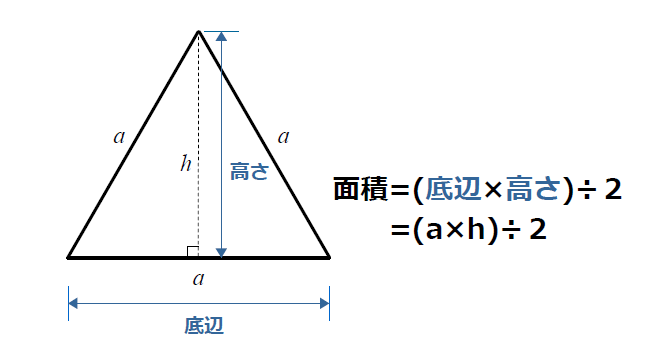
面積の公式 sin
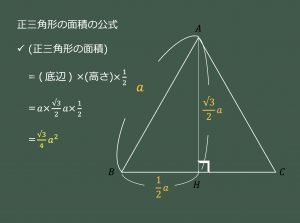
面積の公式 sin-半径 $r$ の円の面積 $S$ は、次の公式で求められます。 円 (えん) の面積 \begin{align*} S = \pi r^2 \end{align*} 面積 = 半径 × 半径 × 314 公式の 導出 (どうしゅつ) 方法と計算 例 (れい) は「円の面 「三角形の面積の求め方」 について、まずは基本から入り、徐々に高校数学の内容に進化させていきます。 具体的には、数学Ⅰで習う "sin" を用いる公式や、数学Bで習う "ベクトル" を

高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
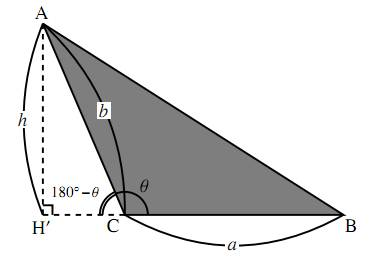
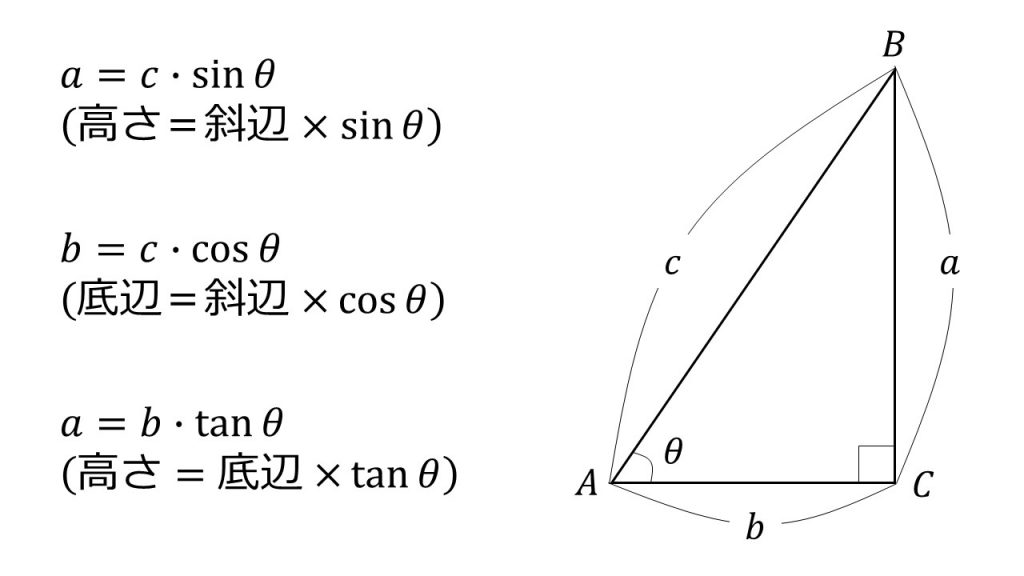
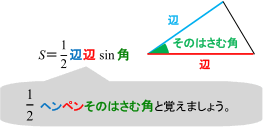
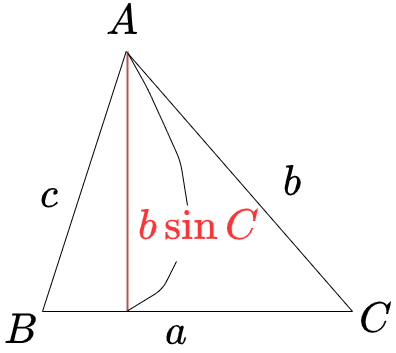
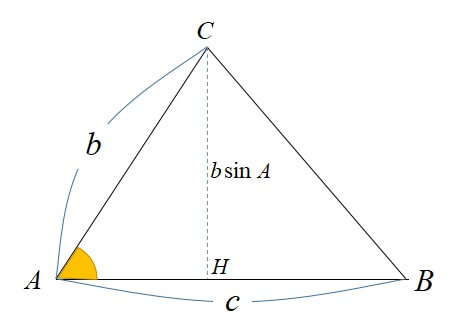
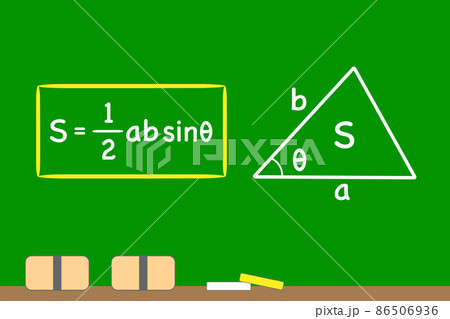
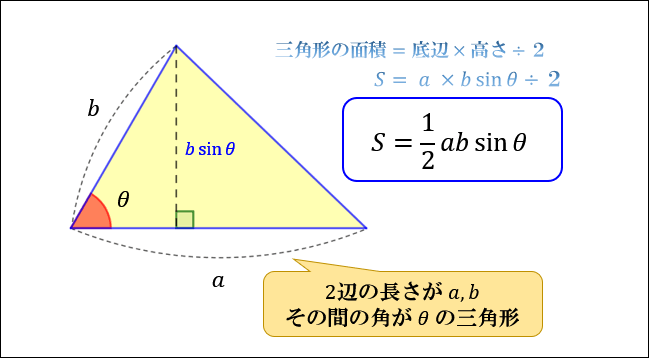
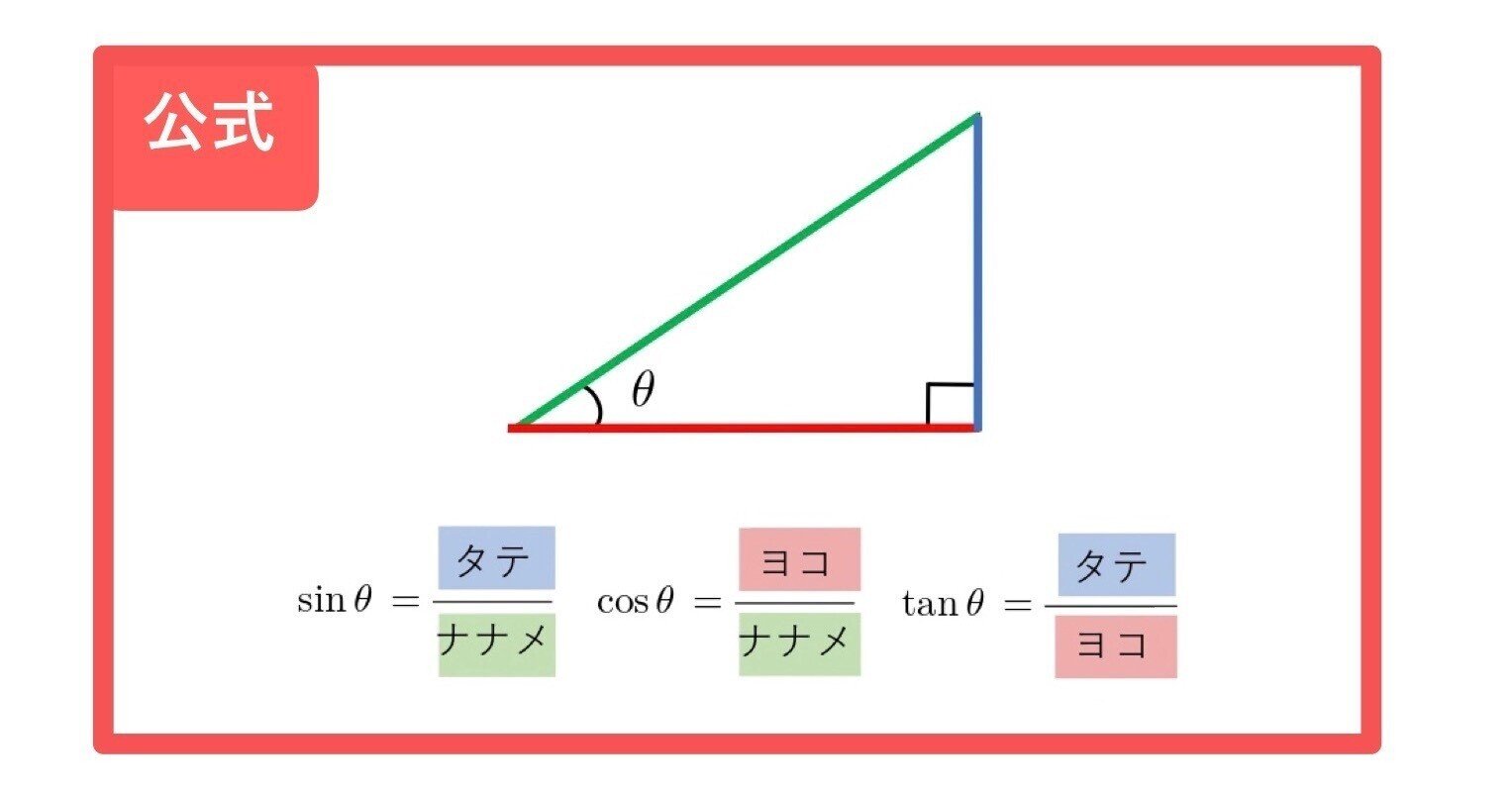
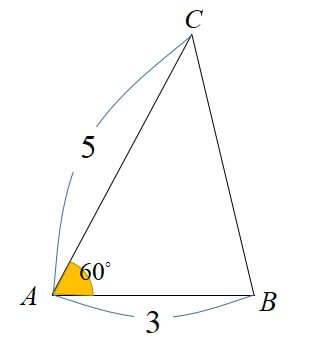
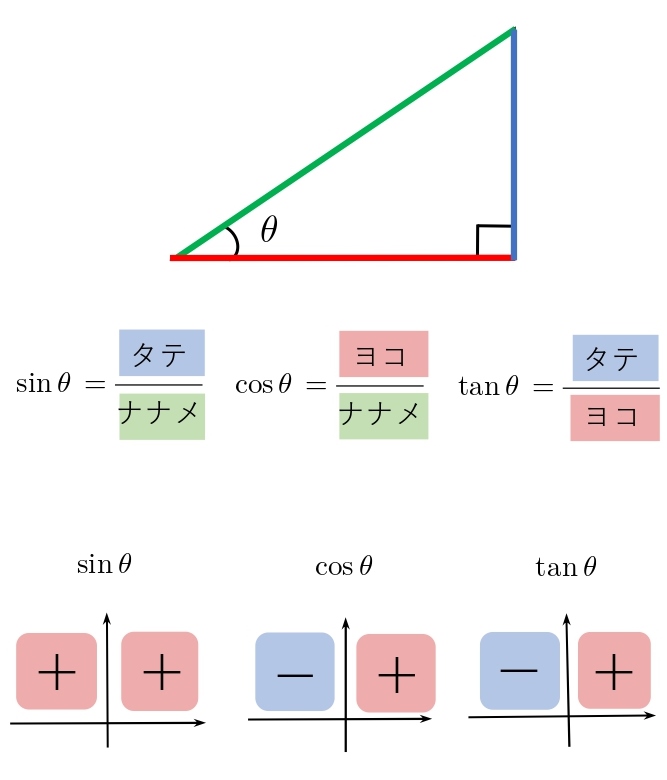
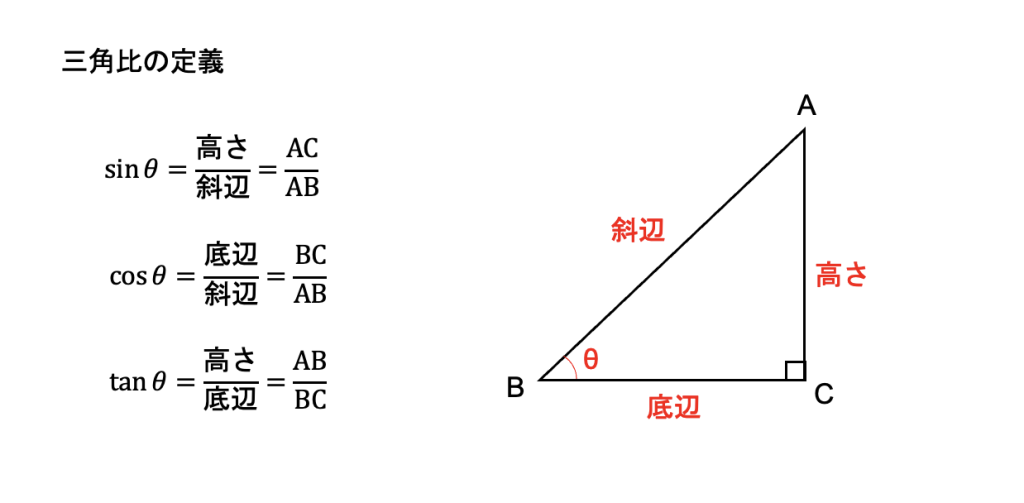
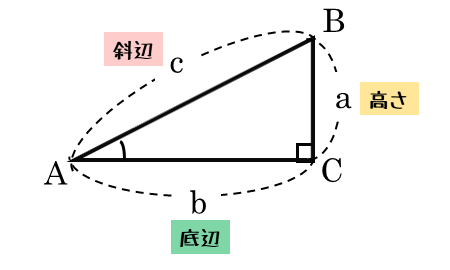
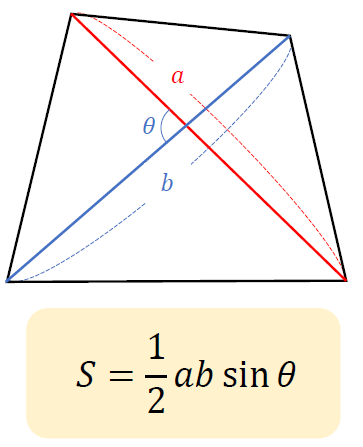
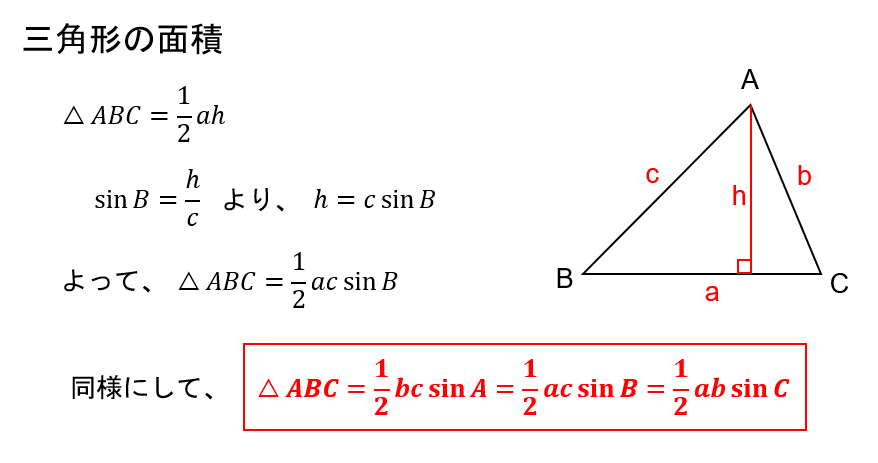
Sinθで三角形のたての長さと面積を計算する 三角比を利用することによって、三角形の面積を計算することができます。 公式としては以下になります。 2辺とその間にある角度がわかっている場合 3 ベクトルの平行四辺形の面積公式 三角形oabの面積をベクトルを用いて表せたら、平行四辺形oacbの面積も簡単に導出できます。 平行四辺形の対角線を引くと、合同な三角形が 2Sin 30 ∘ = cos 60 ∘ 、 cos 30 ∘ = sin 60 ∘ 、 tan 30 ∘ = 1 tan 60 ∘ という関係があります。 より一般に, sin θ = cos ( 90 ∘ − θ) 、 tan θ = 1 tan ( 90 ∘ − θ) という公式が成立します。 ・15度や18度
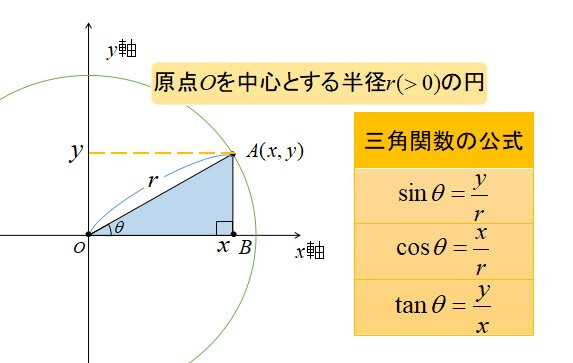
積分 sinθ の図形による理解 ∫ sinθdθ ∫ sin θ d θ の積分を図形を用いて直感的に理解する. 左側の図は 単位円 ,右側の図は y =sinθ y = sin θ のグラフである. 図において赤色の面積と青色の面積 ヘロンの公式は三角比と一緒に習う公式で、三角形の3辺の長さから面積を求める公式です。 ヘロンの公式 三角形ABC 三角形ABCの辺の長さをa, b, cとすると、面積Sは下記の式で表これらは sin (θ), cos (θ) または 括弧 を略して sin θ, cos θ と記述される( θ は対象となる角の大きさ)。 正弦関数と余弦関数の比を正接関数(タンジェント、tangent)と言い、具体的には以下の
面積の公式 sinのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 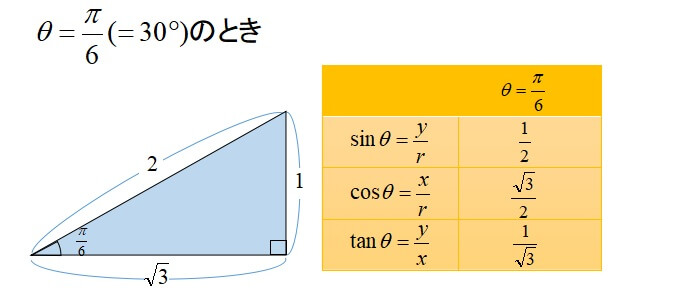 |
「面積の公式 sin」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
たとえば、「4辺の長さがそれぞれ 5, 15, 8, 12 で1組の対角の和が 150 ° の四角形」の面積は、ブレートシュナイダーの公式を使うことで 30 30 3 ≒ 8196 と求まります。 ただし面積の計算 ご意見・ご感想 ヘロンの公式を思い出し手計算を行いこのサイトで確認してみました。 a=103 b=635 c=425 で3615程度になるはずが6315というおかしな計算結果になるのはなぜで
Incoming Term: 面積の公式 sin,




0 件のコメント:
コメントを投稿