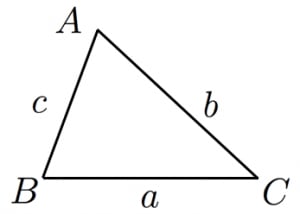
正弦定理(The Law of Sines)是三角学中的一个基本定理,它指出"在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍",即a/sinA = b/sinB =c/sinC = 2r=D(r为外接圆半径,D为直径)。 正弦定理的公式: 在任意 ABC中,角A、B、C所对的三角形边长的计算方法 对于任意一个三角形,已知两角一对边,可以根据正弦定理计算a=b*sinA/sinB。 正弦定理的公式为a/sinA = b/sinB =c/sinC,根据正弦定理的公式可以解三角形。 对于任意一个三角形,已知两条边与夹角,可以根据余弦定理求出第三条边,有公式接下来分享三角形勾股定理公式及证明方法。 三角形勾股定理公式 1基本公式 在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么勾股定理的公式为a ² b ² =c ² 。

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
三角形の定理 公式
三角形の定理 公式-题1: 关于三角形所有定理及概念数学科目 15 定理 三角形两边的和大于第三边 16 推论 三角形两边的差小于第三边 17 三角形内角和定理 三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角このページでは,はじめに, sin ( α β) , cos ( α β) などの ( )をはずす公式 「三角関数の加法定理」 を解説し,その応用として 「2倍角公式」「3倍角公式」「積和の公式」「和積の公式」 を解説する. (1) (2)の証明・・・ (以下の証明は第1象限の




tan8とcos8であらわした三平方の定理の覚え方 Schoolmath S Diary
三角形公式大全 15 定理 三角形两边的和大于第三边 16 推论 三角形两边的差小于第三边 17 三角形内角和定理 三角形三个内角的和等于 180° 18 推论 1 直角三角形的两个锐角互余 19 推论 2 三角形的一个外角等于和它不相邻的两个内角的和 推论 3 三角形的 正弦定理とは何か?2つの視点から分かる公式の覚え方・考え方 三角形 \(abc\) に対して、点 \(a,b,c\) の内角をそれぞれ角 \(a,b,c\) とおき 点 \(a\) の反 三角形中线定理公式 匠子生活 中线定理(Apollonius's theorem),又称阿波罗尼奥斯定理,是欧氏几何的定理,表述三角形三边和中线长度关系。
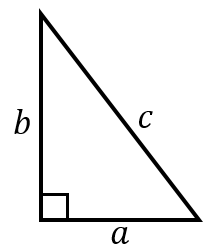
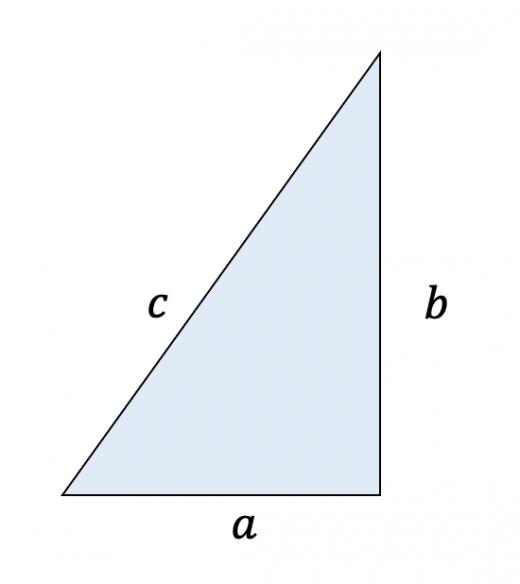
三角形の面積比にまつわる公式たち 三角形の面積比,四面体の体積比にまつわる重要な公式を3 定理:三角形 a b c abc a bc の内接円と辺 b c bc bc の接点を d d d とおく。 d d d から辺 b c bc bc と垂直な直線と内接円の交点を e e e とおく。初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こう公式 在平面一个直角三角形上用直线 a 的平方直线 B 的平方=斜线 C 的平方 这就是勾股定理 经典证明方法细讲 方法一: 作四个全等的直角三角形,设它们的两条直角边长分别为 a、b ,斜边长为 c 把它们拼成如图那样的一个多边形,使 D、E、F 在一条直线上
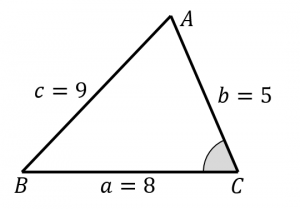
三角形中的诱导公式 正弦定理 余弦定理 面积公式 解三角形常见题型 已知角A,B和边c 已知边a,b与角C 已知边a,b,c 已知边b,c与角C 这种题型可能出现解的个数不定的情况,可结合图形进行判断,也可根据b,c的大小进行判断。 直角三角形とは? 定義や定理、辺の長さの比、合同条件 21年2月19日 この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね三角形ABCの辺BC,CA,ABの長さをa,b,cとし,この三角形の外接円の半径をRとすれば, が成り立つ。 これを正弦定理または正弦法則と呼んでいる(図)。 三角形の一つの辺とその両端の角がわかれば,この公式により他の2辺の長さが計算できるので,この公式は三角法において基本的である。




三平方の定理です この Abcの高さahと面積の求め方を教えてください Clear



名古屋市科学館 科学館を利用する 展示ガイド キーワード検索 さ ではじまるキーワード キーワード 三平方の定理 公式と図形
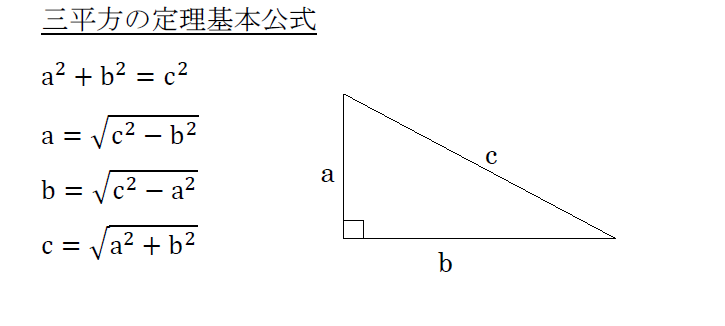
直角三角形の辺の長さを三平方の定理の公式で求めるタイプ。 これは、 三平方の定理の公式に、辺の長さを代入して計算するだけだから簡単だ。 たとえば、つぎの練習問題な。 ピタゴラスの定理とは、古代ギリシアの数学者で哲学者のピタゴラスが立ち上げた団体が発見した数学の定理のこと。直角三角形をなす3辺のうち、2辺の長さを知ることができれば、残り1辺の長さを知ることができるというものです。 公式:a² b² = c² ピタゴラスの定理 とも呼ばれてるやつね。 発見者の名前がついてるわけ。 この三平方の定理(ピタゴラスの定理)とは何かっていうと、 直角三角形の3つの辺の関係を表した公式 なんだ。 もうちょっと具体的にいうと、直角三角形には、




余弦定理で角度を求める方法 数学の星



余弦定理とは 公式の覚え方や証明 計算問題の解き方 受験辞典
初等数学公式集 出典 フリー教科書『ウィキブックス(Wikibooks)』 ナビゲーションに移動 検索に移動 " 公式とは、数式で表される定理のことである " ( 出典フリー百科事典『ウィキペディア(Wikipedia)』 公式 ) 以下に、日本の数学教育において大学三角形の証明・形状問題 → 携帯版は別頁 → 印刷用PDF版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「 加法定理は覚える,他は作る」 というのが,作者おすすめの考え方です そして、三角形の内角の和が180度であることも、問題を解く時によく使いますので、頭の片隅に入れておいてください。 正弦定理の証明 では次に、正弦定理の公式を証明していきます。 正弦定理




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
正弦定理を三角形の面積と関連付けます。 ※ 図は Markdown に SVG を直接記述しています。詳細はこちらをご参照ください。 正弦定理 図 1 A B C 2R a b c 教科書でよく見る形の正弦定理は、円の直径との関係を含んだ形で記述されます。数学 正弦定理 求三角形面积 2;ブレードシュナイダーの公式ってマイナーなのかなぁ。 任意の三角形に対する面積の公式をヘロンの公式と言います。(とっても有名) maths=\displaystyle\frac{abc}{2}/math としたとき、三角形の面積Sは mathS=\sqrt{s(sa)(sb)(sc)}/math で表されます。 〜少し趣味の世界〜 円に内接する任意の四角形に



Sinを用いた三角形の面積公式 高校数学の美しい物語




二辺挟角から残りの辺を求める Schoolmath S Diary
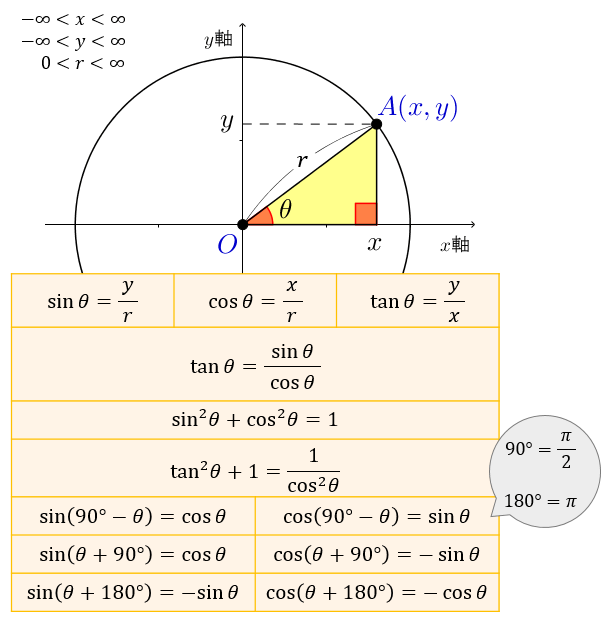
頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b 三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:
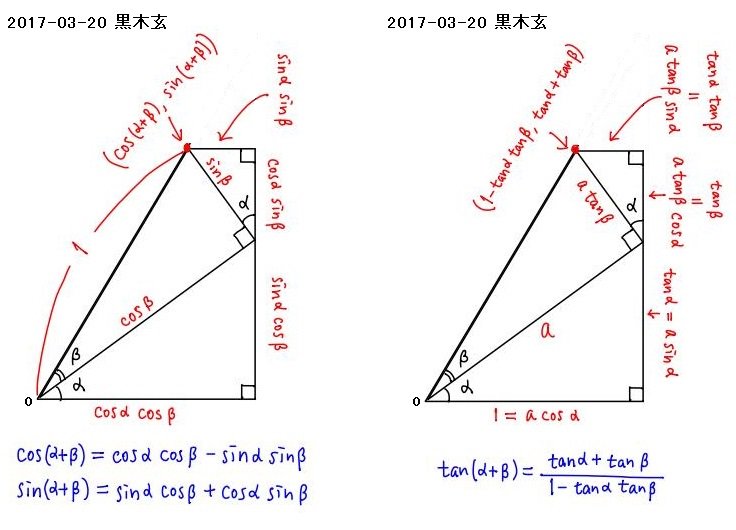



三角函数の加法公式




tan8とcos8であらわした三平方の定理の覚え方 Schoolmath S Diary



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




三平方の定理の証明と使い方




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より



1




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理で辺を求める Youtube



1




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学



1
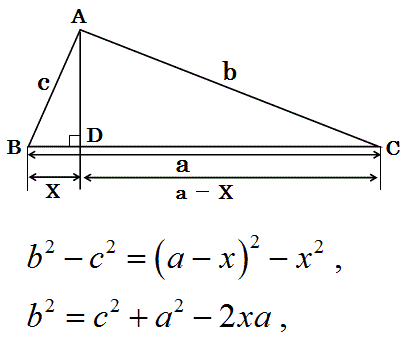



勉強しよう数学 拡張三平方の定理



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



三平方の定理 方程式を利用する発展問題を解説 数スタ




山と数学 そして英語 三平方の定理と三角形の面積 さらに三角比 ヘロンの公式




数学 中3 61 三平方の定理 基本編 Youtube




高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook



直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学




三平方の定理 覚えておきたい基本公式を解説 数スタ




高校入試対策数学 三平方の定理と関数の融合問題 Pikuu



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




โน ตของ 中学数学 三平方の定理を使う問題 平面図形 ช น Clear




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



直角三角形の定義とさまざまな公式 高校数学の美しい物語




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




余弦定理の公式をマスターしよう スタディクラブ情報局




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ



三角形の公式 Wakatta




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理の証明と使い方




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題




三平方の定理の応用




直角三角形の辺を求める Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




直角三角形の辺の長さ 合同条件 面積について アタリマエ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



三角形の面積を3辺の長さから求める2つの方法 具体例で学ぶ数学




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三平方の定理 の問題のわからないを5分で解決 映像授業のtry It トライイット




わかりやすい三角比と基本公式 Irohabook




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




中3数学 三平方の定理の応用 75度に要注意 Youtube




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に
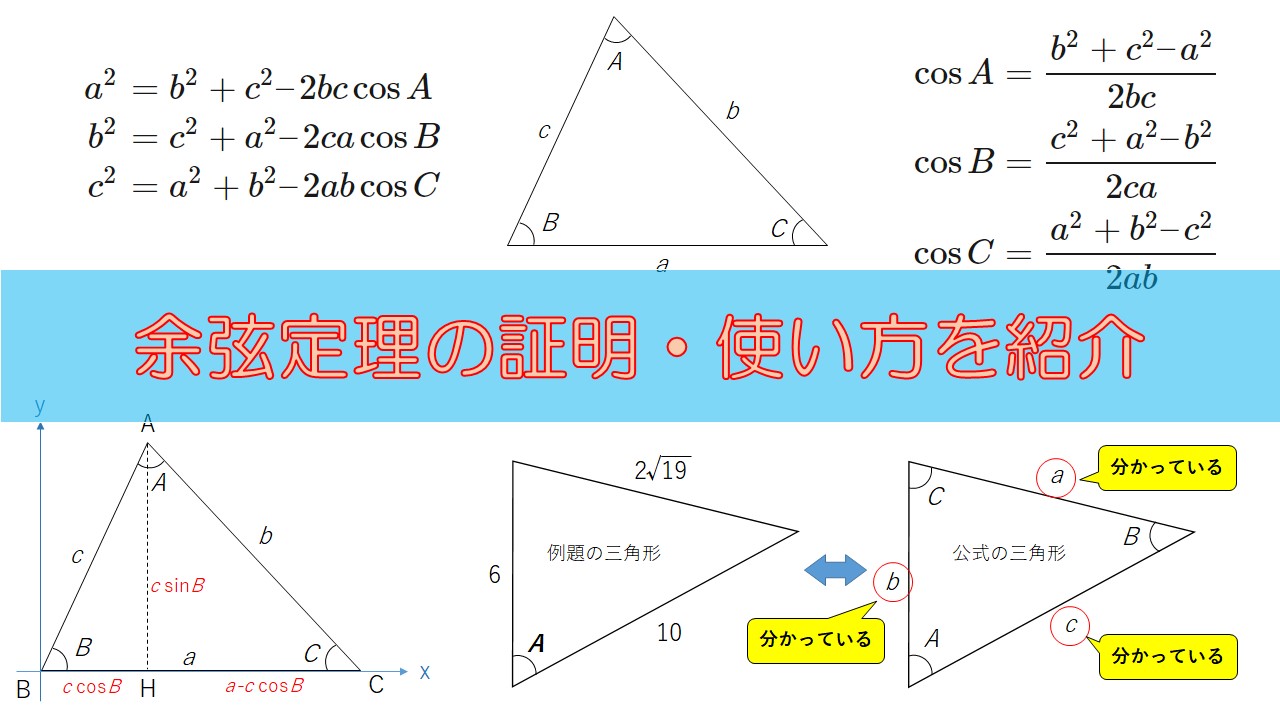



高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく
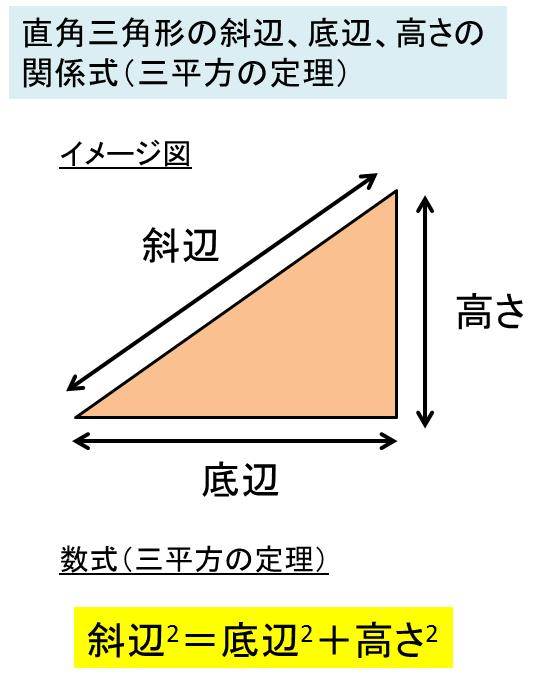



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方



三平方の定理




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




Tossランド 三角比の公式 の暗記プリント Dl可




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
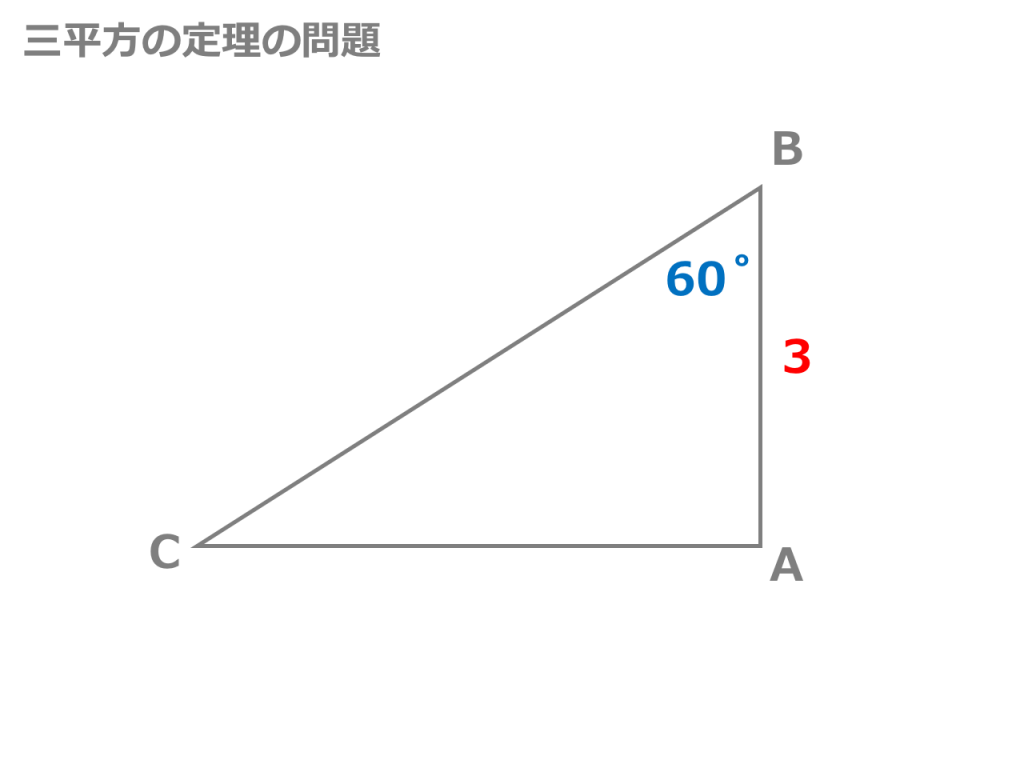



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト
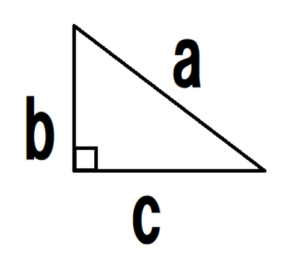



三平方の定理 公式を簡単に覚える方法 中学数学 札幌市 学習塾 受験 チーム個別指導塾 大成会



1




3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest




余弦定理まとめ 公式 面積 問題と解き方 理系ラボ
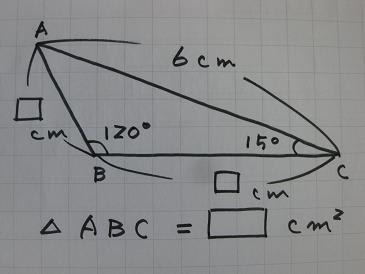



マッキーの教室 中2生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト
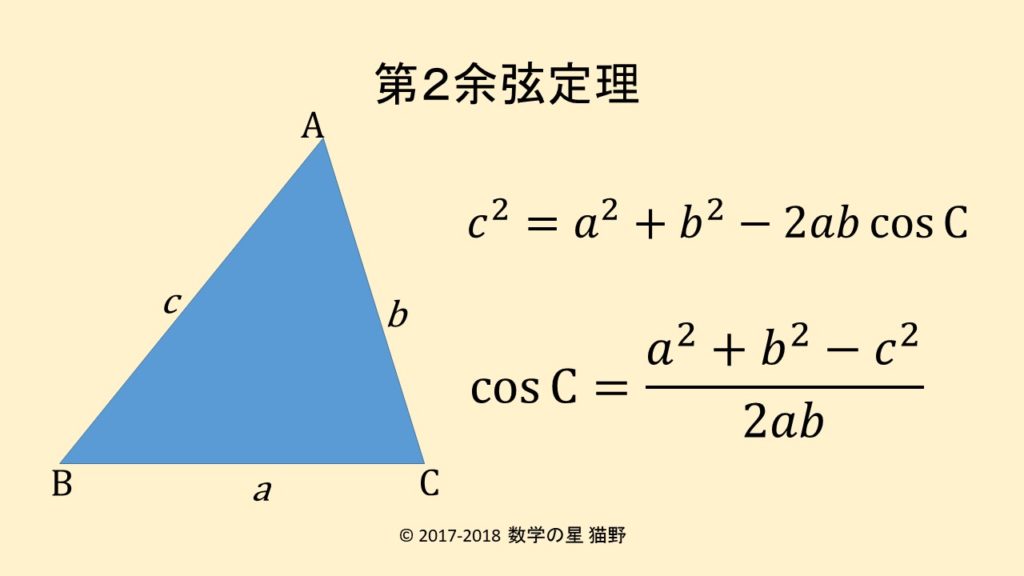



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿